wandelweb.de

S-Kurven sind bekannt und üblich, um Produktlebenszyklen darzustellen.

Natür­liche Wachstums- und Diffusionsprozesse, Epidemien, Wirtschaftszyklen … folgen S-Kurven. In all diesen Fällen liegen zwei gegenläufige Dynamiken vor:

1. eine verstärkende Rückkopplung, die das Wachstum bewirkt,
2. eine balancierende Rückkopplung, die für das Abbremsen sorgt. [1]

Die balancierende Rückkopplung wird durch den Minimumfaktor oder Engpass bestimmt. Mit zunehmendem Wachstum wird er immer knapper und bringt schließlich das Wachstum zum Stillstand.

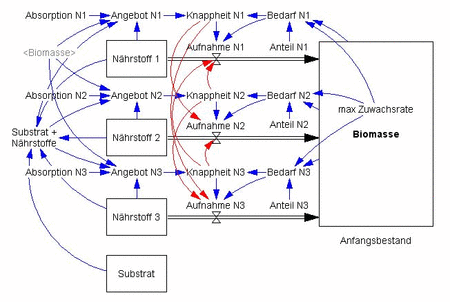
Im einem einfachen System-Dynamics-Modell [2] habe ich ein geschlossenes System für das Wachstum einer Pflanze simuliert. Die Pflanze wächst in einem Substrat, in dem drei Nährstoffe in unterschiedlichen Konzentrationen vorliegen, die unter­schiedlich schnell absorbiert werden können. Die Pflanze braucht diese Nährstoffe zu bestimmten Anteilen. Bei Knappheit eines Nährstoffes kann die Pflanze auch die anderen Nährstoffe entsprechend langsamer aufnehmen.

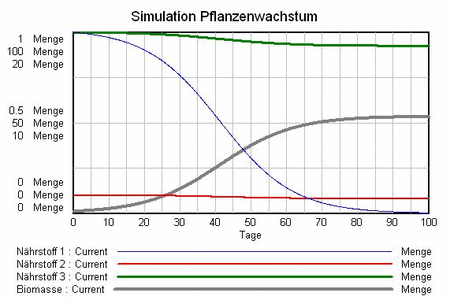
Stagnation trotz Überschuss an Ressourcen

Die Simulation zeigt, dass das Pflanzenwachstum S-förmig verläuft. Nährstoff 1 ist der Minimumfaktor. Obwohl er in der geringsten Menge benötigt wird, bringt er das Pflanzenwachstum zum Erliegen. Das zeigt uns, dass auch sehr kleine Faktoren zum Engpass werden können.

Die anderen Faktoren (Nährstoffe 2 und 3) sind im Überschuss vorhanden. Wenn wir jetzt diese anderen Faktoren reduzieren (Effizienzprogramm), wird die Pflanze nicht schneller wachsen. Im Gegenteil riskieren wir, das Pflanzenwachstum noch weiter einzuschränken [3]. Entgegen dem gängigen Verständnis haben Effizienz­programme ohne gleichzeitiges Engpassmanagement also kaum, oft sogar gegen­teilige Wirkungen.

Die einzig richtige Methode für effektiven Mitteleinsatz ist, unserer „Pflanze“ mehr von Nährstoff 1, dem Engpassfaktor zuzuführen. Durch gezielten Fokus auf den Engpass kann also auch für bestehende Produkte mit kleinem Aufwand Verblüffendes bewirkt werden. Ohne gezieltes Engpassmanagement können bestehende Produkte (Pflanzen, Lebewesen) ihre Wachstumspotenziale meistens nicht ausschöpfen. Allerdings ist es oft nicht ganz leicht, den jeweiligen Engpass­faktor zu entdecken.

Engpassmanagement und Unternehmensstrategie

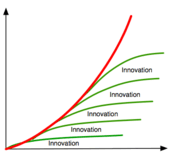
Produkte haben wie Populationen natürliche Wachstumsgrenzen, die erreicht werden, wenn der Bedarf gesättigt ist. Sicher lassen sich durch Verbesserungen und partielle Innovationen die Wachstumsgrenzen verschieben, aber nur einge­schränkt und mit immer mehr Aufwand.

Der richtige Weg für Unternehmen ist also, sich nicht endgültig auf ein bestimmtes Produkt festzulegen, sondern sich und die Produkte an den langfristigen Grundbedürfnissen ihrer Kunden auszurichten. Innovation bedeutet hier, neue und andersartige Produkte und Dienstleistungen anzubieten, die bisher noch nicht angeboten werden und damit neue Nischen und Märkte eröffnen. Engpass­management erstreckt sich also auch auf die Unternehmensstrategie.